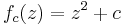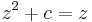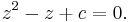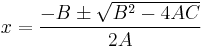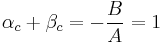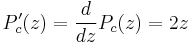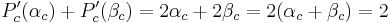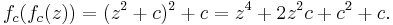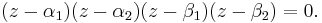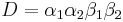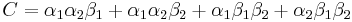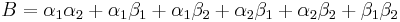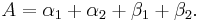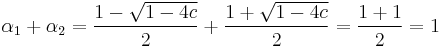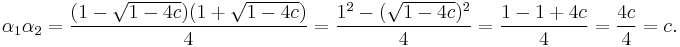Periodic points of complex quadratic mappings

This article describes periodic points of some complex quadratic maps. A map is a formula for computing a value of a variable based on its own previous value or values; a quadratic map is one that involves the previous value raised to the powers one and two; and a complex map is one in which the variable is a complex number. A periodic point of a map is a value of the variable that occurs repeatedly after intervals of a fixed length.

This theory is applied in relation with the theories of Fatou and Julia sets.

1 Definitions
2 Stability of periodic points (orbit) - multiplier
3 Period-1 points (fixed points)
- 3.1 Finite fixed points
- 3.2 Infinite fixed point
4 Period-2 cycles
- 4.1 first method
- 4.2 Second method of factorization
  - 4.2.1 Special cases
5 Cycles for period>2
6 References
7 Further reading
8 External links

Definitions

Let

$f_c(z)=z^2%2Bc\,$

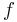where $z$ and $c$ are complex-valued. (This $\ f$ is the complex quadratic mapping mentioned in the title.) This article explores the periodic points of this mapping - that is, the points that form a periodic cycle when 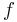$\ f$ is repeatedly applied to them.

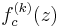$\ f^{(k)} _c (z)$ is the 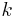$\ k$ -fold compositions of 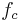$f _c\,$ with itself = iteration of function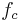 $f _c\,$

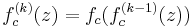
$\ f^{(k)} _c (z) = f_c(f^{(k-1)} _c (z))$

then periodic points of complex quadratic mapping of period 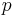$\ p$ are points 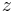$\ z$ of dynamical plane such that :

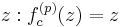
$\ z�: f^{(p)} _c (z) = z$

where 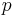$\ p$ is the smallest positive integer.

We can introduce new function:

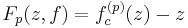
$\ F_p(z,f) = f^{(p)} _c (z) - z$

so periodic points are zeros of function 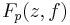$\ F_p(z,f)$ :

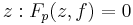
$\ z�: F_p(z,f) = 0$

which is polynomial of degree 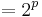$\ = 2^p$

Stability of periodic points (orbit) - multiplier

The multiplier ( or eigenvalue, derivative ) 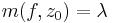$m(f,z_0)=\lambda \,$ of rational map 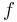$f\,$ at fixed point 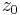$z_0\,$ is defined as :

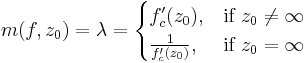
$m(f,z_0)=\lambda = \begin{cases} f_c'(z_0), &\mbox{if }z_0\ne \infty \\ \frac{1}{f_c'(z_0)}, & \mbox{if }z_0 = \infty \end{cases}$

where 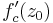$f_c'(z_0)\,$ is first derivative of 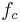$\ f_c$ with respect to 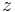$z\,$ at $z_0\,$ .

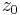Because the multiplier is the same at all periodic points, it can be called a multiplier of periodic orbit.

Multiplier is:

complex number,
invariant under conjugation of any rational map at its fixed point^[1]
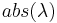
used to check stability of periodic (also fixed) points with stability index : $abs(\lambda) \,$

Periodic point is :^[2]

attracting when
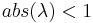
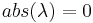
- super-attracting when $abs(\lambda) = 0 \,$
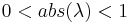
- attracting but not super-attracting when $0 < abs(\lambda) < 1 \,$
indifferent when
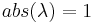
- rationally indifferent if 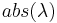$abs(\lambda) \,$ is a root of unity
- irrationally indifferent if 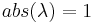$abs(\lambda)=1 \,$ but multiplier is not a root of unity
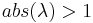
repelling when $abs(\lambda) > 1 \,$

Where do periodic points belong?

attracting is always in Fatou set
repelling is in the Julia set
Indifferent fixed points may be in the one or in the other ^[3]

Period-1 points (fixed points)

Finite fixed points

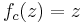Let us begin by finding all finite points left unchanged by 1 application of $f$ . These are the points that satisfy $\ f_c(z)=z$ . That is, we wish to solve

$z^2%2Bc=z\,$

which can be rewritten

$\ z^2-z%2Bc=0.$

Since this is an ordinary quadratic equation in 1 unknown, we can apply the standard quadratic solution formula. Look in any standard mathematics textbook, and you will find that there are two solutions of 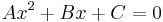$\ Ax^2%2BBx%2BC=0$ are given by

$x=\frac{-B\pm\sqrt{B^2-4AC}}{2A}$

In our case, we have 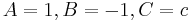$A=1, B=-1, C=c$ , so we will write

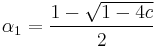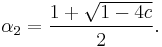
$\alpha_1 = \frac{1-\sqrt{1-4c}}{2}$ and $\alpha_2 = \frac{1%2B\sqrt{1-4c}}{2}.$

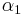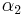So for $c \in C \setminus [1/4,%2B\inf ]$ we have two finite fixed points $\alpha_1 \,$ and $\alpha_2\,$ .

Since

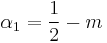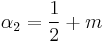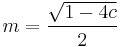
$\alpha_1 = \frac{1}{2}-m$ and $\alpha_2 = \frac{1}{2}%2B m$ where $m = \frac{\sqrt{1-4c}}{2}$

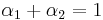then $\alpha_1 %2B \alpha_2 = 1 \,$ .

It means that fixed points are symmetrical around 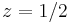$z = 1/2\,$ .

Complex dynamics

Here different notation is commonly used:^[4]

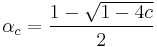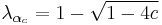
$\alpha_c = \frac{1-\sqrt{1-4c}}{2}$ with multiplier $\lambda_{\alpha_c} = 1-\sqrt{1-4c}\,$

and

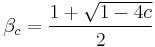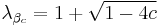
$\beta_c = \frac{1%2B\sqrt{1-4c}}{2}$ with multiplier $\lambda_{\beta_c} = 1%2B\sqrt{1-4c}\,$

Using Viète's formulas one can show that:

$\alpha_c %2B \beta_c = -\frac{B}{A} = 1$

Since derivative with respect to z is :

$P_c'(z) = \frac{d}{dz}P_c(z) = 2z$

then

$P_c'(\alpha_c) %2B P_c'(\beta_c)= 2 \alpha_c %2B 2 \beta_c = 2 (\alpha_c %2B \beta_c) = 2 \,$

It implies that 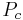$P_c \,$ can have at most one attractive fixed point.

This points are distinguished by the facts that:

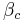is :
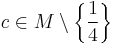
- the landing point of external ray for angle=0 for $c \in M \setminus \left \{ \frac{1}{4} \right \}$
- the most repelling fixed point, belongs to Julia set,
- the one on the right ( whenever fixed point are not symmetrical around the real axis), it is the extreme right point for connected Julia sets (except for cauliflower).^[5]
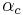is:
- landing point of several rays
- is :
  - attracting when c is in main cardioid of Mandelbrot set, then it is in interior of Filled-in Julia set, it means belongs to Fatou set ( strictly to basin of attraction of finite fixed point )
  - parabolic at the root point of the limb of Mandelbtot set
  - repelling for other c values

Special cases

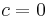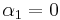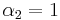An important case of the quadratic mapping is $c=0$ . In this case, we get $\alpha_1 = 0$ and $\alpha_2=1$ . In this case, 0 is a superattractive fixed point, and 1 belongs to the Julia set.

Only one fixed point

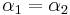We might wonder what value $c$ should have to cause $\alpha_1=\alpha_2$ . The answer is that this will happen exactly when 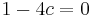$1-4c=0$ . This equation has 1 solution: 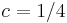$c=1/4$ (in which case, 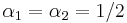$\alpha_1=\alpha_2=1/2$ ). This is interesting, since 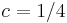$c=1/4$ is the largest positive, purely-real value for which a finite attractor exists.

Infinite fixed point

We can extend complex plane 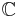$\mathbb{C}$ to Riemann sphere (extended complex plane) 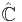$\mathbb{\hat{C}}$ by adding infinity

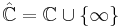
$\mathbb{\hat{C}} = \mathbb{C} \cup \{ \infty \}$

and extend polynomial 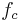$f_c\,$ such that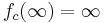 $f_c(\infty)=\infty\,$

Then infinity is :

superattracting
fixed point of polynomial 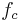$f_c\,$ ^[6]

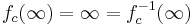
$f_c(\infty)=\infty=f^{-1}_c(\infty)\,$

Period-2 cycles

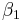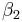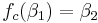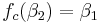Suppose next that we wish to look at period-2 cycles. That is, we want to find two points $\beta_1$ and $\beta_2$ such that $f_c(\beta_1) = \beta_2$ , and $f_c(\beta_2) = \beta_1$ .

Let us start by writing 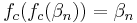$f_c(f_c(\beta_n)) = \beta_n$ , and see where trying to solve this leads.

$f_c(f_c(z)) = (z^2%2Bc)^2%2Bc = z^4 %2B 2z^2c %2B c^2 %2B c.\,$

Thus, the equation we wish to solve is actually 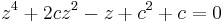$z^4 %2B 2cz^2 - z %2B c^2 %2B c = 0$ .

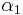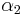This equation is a polynomial of degree 4, and so has 4 (possibly non-distinct) solutions. However, actually, we already know 2 of the solutions. They are $\alpha_1$ and $\alpha_2$ , computed above. It is simple to see why this is; if these points are left unchanged by 1 application of $f$ , then clearly they will be unchanged by 2 applications (or more).

Our 4th-order polynomial can therefore be factored in 2 ways :

first method

$(z-\alpha_1)(z-\alpha_2)(z-\beta_1)(z-\beta_2) = 0.\,$

This expands directly as 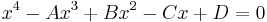$x^4 - Ax^3 %2B Bx^2 - Cx %2B D = 0$ (note the alternating signs), where

$D = \alpha_1 \alpha_2 \beta_1 \beta_2\,$

$C = \alpha_1 \alpha_2 \beta_1 %2B \alpha_1 \alpha_2 \beta_2 %2B \alpha_1 \beta_1 \beta_2 %2B \alpha_2 \beta_1 \beta_2\,$

$B = \alpha_1 \alpha_2 %2B \alpha_1 \beta_1 %2B \alpha_1 \beta_2 %2B \alpha_2 \beta_1 %2B \alpha_2 \beta_2 %2B \beta_1 \beta_2\,$

$A = \alpha_1 %2B \alpha_2 %2B \beta_1 %2B \beta_2.\,$

We already have 2 solutions, and only need the other 2. This is as difficult as solving a quadratic polynomial. In particular, note that

$\alpha_1 %2B \alpha_2 = \frac{1-\sqrt{1-4c}}{2} %2B \frac{1%2B\sqrt{1-4c}}{2} = \frac{1%2B1}{2} = 1$

and

$\alpha_1 \alpha_2 = \frac{(1-\sqrt{1-4c})(1%2B\sqrt{1-4c})}{4} = \frac{1^2 - (\sqrt{1-4c})^2}{4}= \frac{1 - 1 %2B 4c}{4} = \frac{4c}{4} = c.$

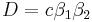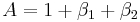Adding these to the above, we get $D = c \beta_1 \beta_2$ and $A = 1 %2B \beta_1 %2B \beta_2$ . Matching these against the coefficients from expanding $f$ , we get

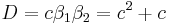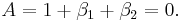
$D = c \beta_1 \beta_2 = c^2 %2B c$ and $A = 1 %2B \beta_1 %2B \beta_2 = 0.$

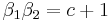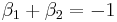From this, we easily get : $\beta_1 \beta_2 = c %2B 1$ and $\beta_1 %2B \beta_2 = -1$ .

From here, we construct a quadratic equation with 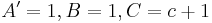$A' = 1, B = 1, C = c%2B1$ and apply the standard solution formula to get

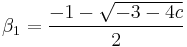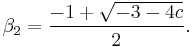
$\beta_1 = \frac{-1 - \sqrt{-3 -4c}}{2}$ and $\beta_2 = \frac{-1 %2B \sqrt{-3 -4c}}{2}.$

Closer examination shows (the formulas are a tad messy) that :

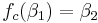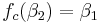
$f_c(\beta_1) = \beta_2$ and $f_c(\beta_2) = \beta_1$

meaning these two points are the two halves of a single period-2 cycle.

Second method of factorization

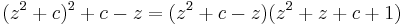
$(z^2%2Bc)^2 %2B c -z = (z^2 %2B c - z)(z^2 %2B z %2B c %2B1 ) \,$

The roots of the first factor are the two fixed points 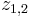$z_{1,2}\,$ . They are repelling outside the main cardioid.

The second factor has two roots

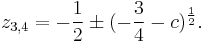
$z_{3,4} = -\frac{1}{2} \pm (-\frac{3}{4} - c)^\frac{1}{2}. \,$

These two roots form period-2 orbit.^[7]

Special cases

Again, let us look at 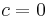$c=0$ . Then

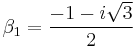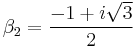
$\beta_1 = \frac{-1 - i\sqrt{3}}{2}$ and $\beta_2 = \frac{-1 %2B i\sqrt{3}}{2}$

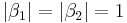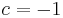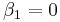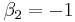both of which are complex numbers. By doing a little algebra, we find $| \beta_1 | = | \beta_2 | = 1$ . Thus, both these points are "hiding" in the Julia set. Another special case is $c=-1$ , which gives $\beta_1 = 0$ and $\beta_2 = -1$ . This gives the well-known superattractive cycle found in the largest period-2 lobe of the quadratic Mandelbrot set.

Cycles for period>2

There is no general solution in radicals to polynomial equations of degree five or higher, so it must be computed using numerical methods.

References

^ Alan F. Beardon, Iteration of Rational Functions, Springer 1991, ISBN 0-387-95151-2, p. 41
^ Alan F. Beardon, Iteration of Rational Functions, Springer 1991, ISBN 0-387-95151-2, page 99
^ Some Julia sets by Michael Becker
^ On the regular leaf space of the cauliflower by Tomoki Kawahira Source: Kodai Math. J. Volume 26, Number 2 (2003), 167-178.
^ Periodic attractor by Evgeny Demidov
^ R L Devaney, L Keen (Editor): Chaos and Fractals: The Mathematics Behind the Computer Graphics. Publisher: Amer Mathematical Society July 1989, ISBN 0821801376 , ISBN 9780821801376
^ Period 2 orbit by Evgeny Demidov

External links

Algebraic solution of Mandelbrot orbital boundaries by Donald D. Cross
Brown Method by Robert P. Munafo
arXiv:hep-th/0501235v2 V.Dolotin, A.Morozov: Algebraic Geometry of Discrete Dynamics. The case of one variable.
Gvozden Rukavina : Quadratic recurrence equations - exact explicit solution of period four fixed points functions in bifurcation diagram

Periodic points of complex quadratic mappings

Contents

Definitions

Stability of periodic points (orbit) - multiplier

Period-1 points (fixed points)

Finite fixed points

Complex dynamics

Special cases

Only one fixed point

Infinite fixed point

Period-2 cycles

first method

Second method of factorization

Special cases

Cycles for period>2

References

Further reading

External links